IIR Least-Squares Estimate

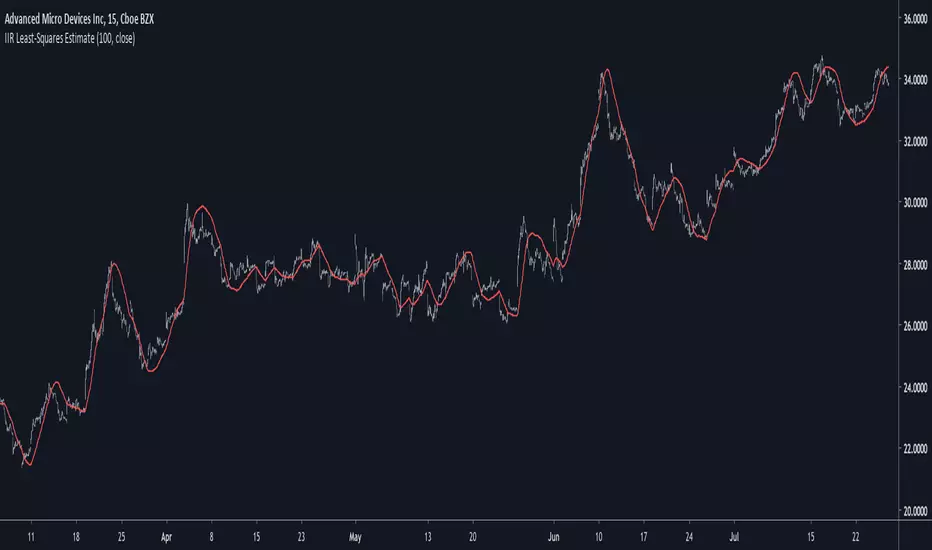
Introduction

Another lsma estimate, i don't think you are surprised, the lsma is my favorite low-lag filter and i derived it so many times that our relationship became quite intimate. So i already talked about the classical method, the line-rescaling method and many others, but we did not made to many IIR estimate, the only one was made using a general filter estimator and was pretty inaccurate, this is why i wanted to retry the challenge.

Before talking about the formula lets breakdown again what IIR mean, IIR = infinite impulse response, the impulse response of an IIR filter goes on forever, this is why its infinite, such filters use recursion, this mean they use output's as input's, they are extremely efficient.

The Calculation

The calculation is made with only 1 pole, this mean we only use 1 output value with the same index as input, more poles often means a transition band closer to the cutoff frequency.

Our filter is in the form of :

y = a*x+y - a*ema(y,length/2)

where y = x when t = 1 and y(1) when t > 2 and a = 4/(length+2)

This is also an alternate form of exponential moving average but smoothing the last output terms with another exponential moving average reduce the lag.

Comparison

Lets see the accuracy of our estimate.



Sometimes our estimate follow better the trend, there isn't a clear result about the overshoot/undershoot response, sometimes the estimate have less overshoot/undershoot and sometime its the one with the highest.





The estimate behave nicely with short length periods.

Conclusion

Some surprises, the estimate can at least act as a good low-lag filter, sometimes it also behave better than the lsma by smoothing more. IIR estimate are harder to make but this one look really correct.


If you are looking for something or just want to say thanks try to pm me :)

Thank for reading !